Wurzelfunktionen

Inhaltsverzeichnis zum Thema

• Was ist eine Wurzelfunktion?
  • Wurzelfunktionen als Umkehrfunktionen von Potenzfunktionen
  • Der Definitionsbereich und der Wertebereich einer Wurzelfunktion
  • Eigenschaften von Wurzelfunktionen
• Herleitung von Wurzelfunktionen
  • Die Quadratwurzel als Umkehrung einer quadratischen Funktion
  • Die Kubikwurzel als Umkehrung einer kubischen Funktion
  • Die Umkehrung einer Hyperbelfunktion
• Anwendungsbeispiel

Was ist eine Wurzelfunktion?

Was versteht man unter einer Wurzelfunktion? Eine Wurzelfunktion hat die folgende Form:

$f(x)=\sqrt[n] x$

Merke dir die folgenden Bezeichnungen in einer allgemeinen Wurzel:

• $n\in\mathbb{N}$ wird als Wurzelexponent bezeichnet.
• Das Argument $x$ der Funktion steht unter der Wurzel und wird als Radikand bezeichnet.
• Für gerade Wurzelexponenten muss $x\ge 0$ sein, da man in diesen Fällen nicht die Wurzel aus einer negativen Zahl ziehen kann. ($x^2$, $x^4$, $x^6$, ... verlaufen alle oberhalb der x-Achse.)
• Für ungerade Wurzelexponenten darf $x$ auch negativ sein: $\sqrt[3]{-8} = -2$.

Wurzelfunktionen als Umkehrfunktionen von Potenzfunktionen

Eine Potenzfunktion ist gegeben in der Form $p(x)=x^n$, wobei der Exponent $n$ eine ganze Zahl ist: $n\in\mathbb{Z}$.

• Der Graph von Potenzfunktionen mit natürlichem Exponenten $n$ wird als Parabel der Ordnung $n$ bezeichnet.
• Der Graph von Potenzfunktionen mit negativem ganzzahligen Exponenten $-n$ wird als Hyperbel der Ordnung $n$ bezeichnet.

Eine Wurzelfunktion ist die Umkehrfunktion einer Potenzfunktion. Mathematisch lässt die Umkehrung so beschreiben:

$x^n=y \Leftrightarrow x=\sqrt[n]y$

Jede Wurzelfunktion lässt sich auch als Potenz schreiben. Dies ist manchmal sehr nützlich:

$f(x)=\sqrt[n] x=x^{\frac1n}$

Der Definitionsbereich und der Wertebereich einer Wurzelfunktion

Du darfst im Bereich der reellen Zahlen nicht die Wurzel aus einer negativen Zahl ziehen, wenn der Wurzelexponent gerade ist (s.o.). Das bedeutet dann, dass du für das Argument (die Variable $x$ nicht jeden beliebigen Wert einsetzen kannst. Also ist der Definitionsbereich** einer Wurzelfunktion mit geradem Wurzelexponenten gegeben durch $\mathbb{D}_f=\mathbb{R}_0^+$.

Der Wertebereich einer solchen Wurzelfunktion ist $\mathbb{W}_f=\mathbb{R}_0^+$.

Eigenschaften von Wurzelfunktionen

Welche Eigenschaften können wir für Wurzelfunktionen allgemein beobachten?

• Für positive Wurzelexponenten verläuft der Graph der Wurzelfunktion monoton wachsend.
• Es gilt $\sqrt[n]0=0$ für alle $n\in\mathbb{N}$. Das bedeutet insbesondere, dass bei $x=0$ die einzige Nullstelle einer Wurzelfunktion mit natürlichem Wurzelexponenten liegt.
• Es gilt $\sqrt[n]1=1$ für alle $n\in\mathbb{Z}$.
• Bei der Quadratwurzel wird der Wurzelexponent nicht aufgeschrieben.

Herleitung von Wurzelfunktionen

Nach der ganzen Theorie wollen wir uns nun einige Beispiele spezieller Wurzelfunktionen sowie deren Funktionsgraphen ansehen.

Die Quadratwurzel als Umkehrung einer quadratischen Funktion

Du kannst den Flächeninhalt eines Quadrates berechnen, indem du die Länge der Seite quadrierst.

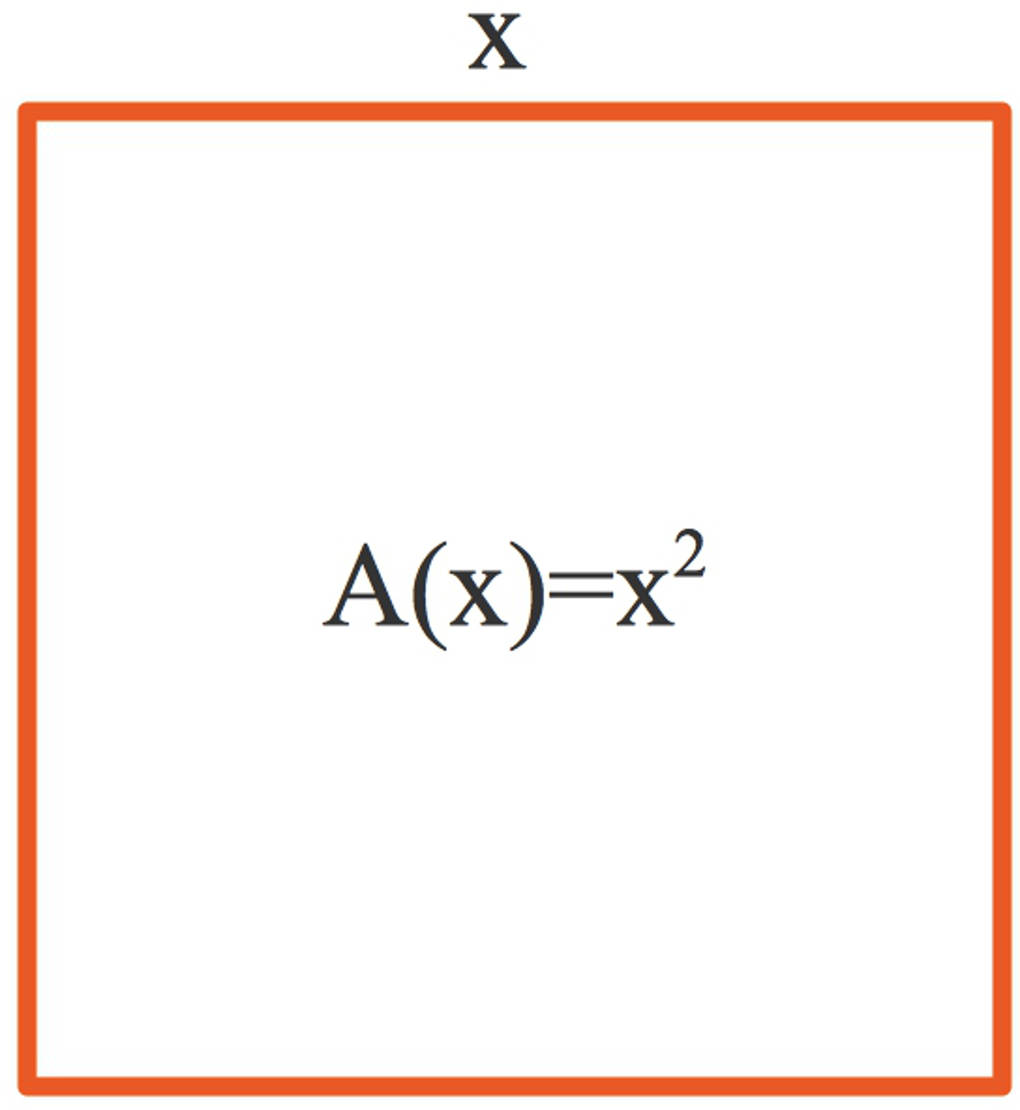
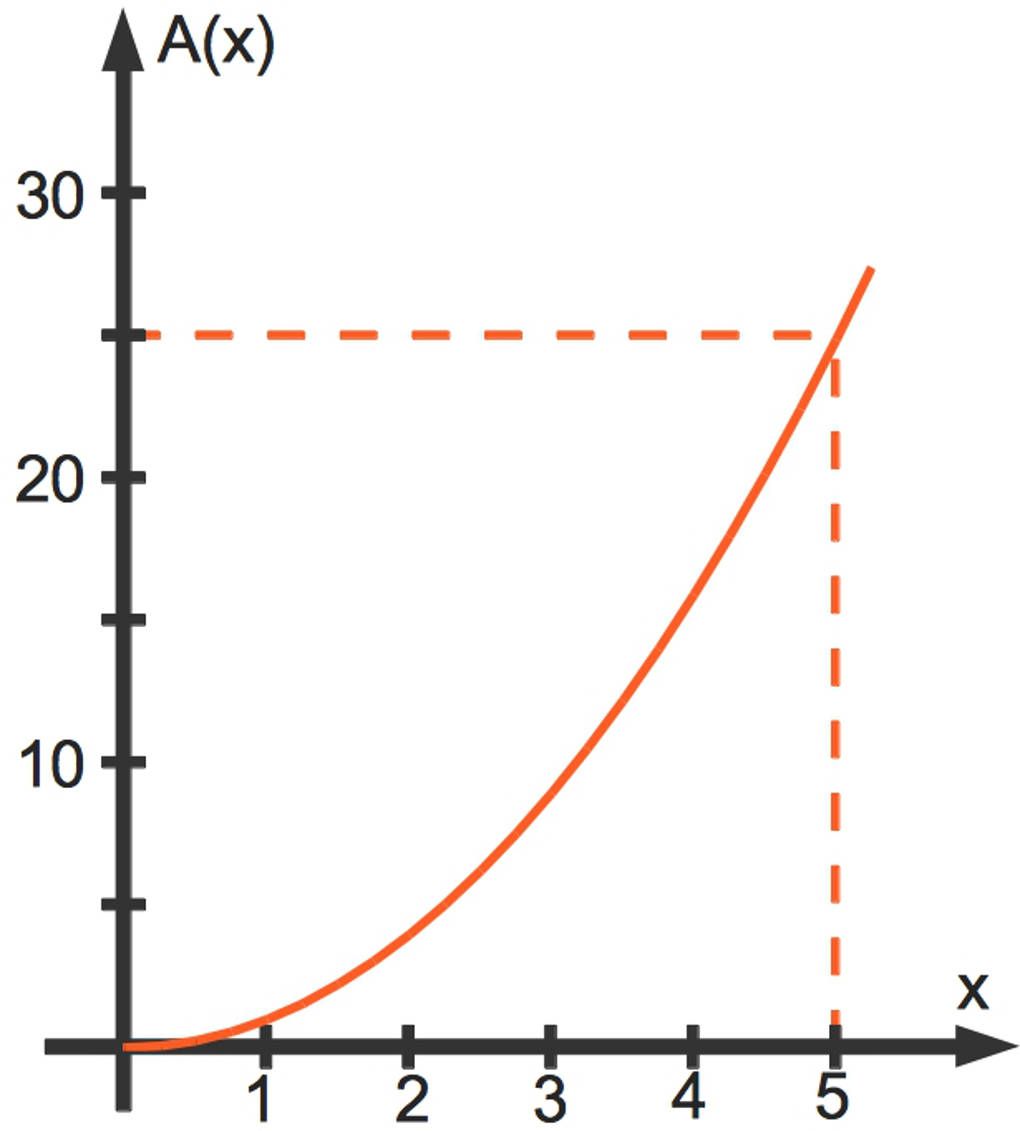
Das bedeutet, dass die quadratische Funktion $A(x)=x^2$ für $x\ge 0$ den jeweils zugehörigen positiven Flächeninhalt angibt. Dabei steht $A(x)$ für den Flächeninhalt (in $\text{cm}^2$) und $x$ für die Seitenlänge (in $\text{cm}$). Hier siehst du den zugehörigen Funktionsgraphen: eine Parabel.

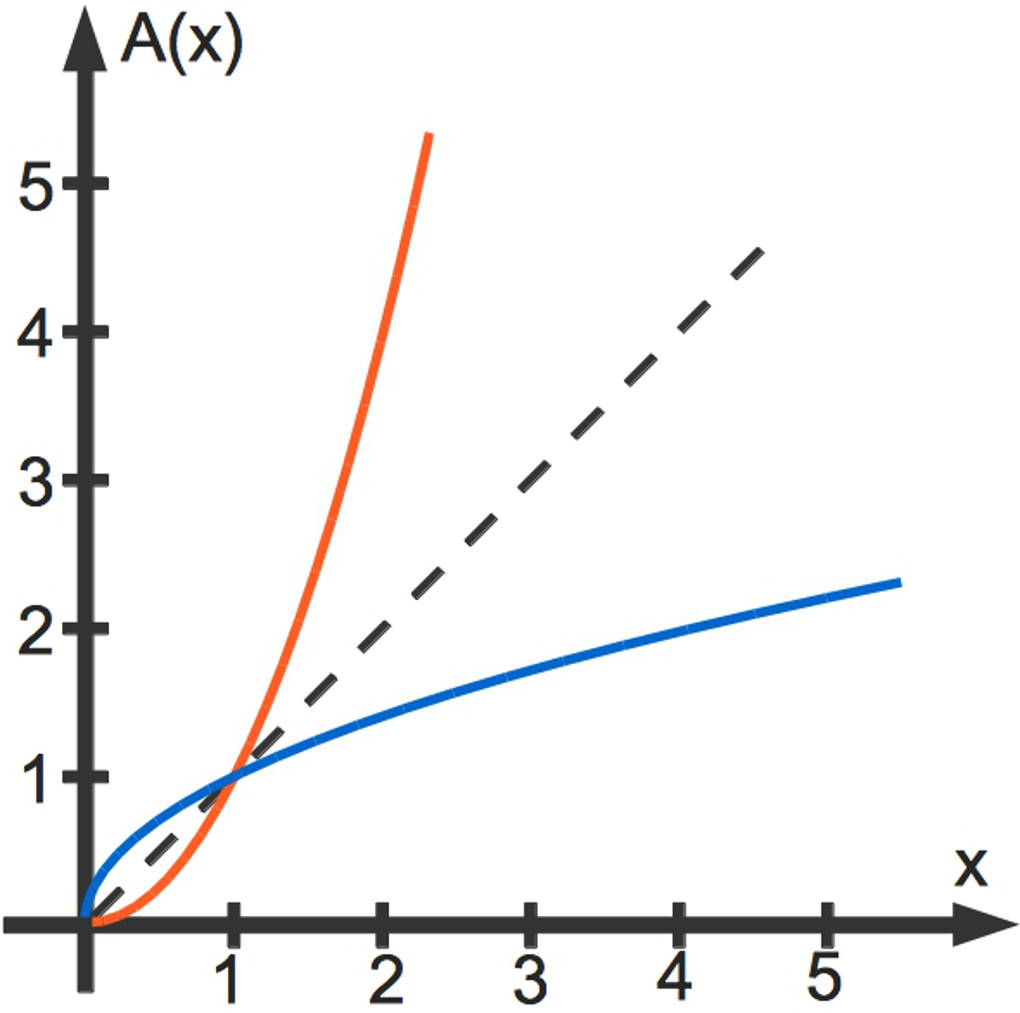
Angenommen ein Quadrat hat den Flächeninhalt $A(x)=25$. Willst du nun umgekehrt wissen, welche Seitenlänge ein Quadrat mit gegebenem Flächeninhalt hat, musst du die Funktion umkehren. Du erhältst den Funktionsgraphen der Umkehrfunktion durch Spiegelung der ursprünglichen Funktion an der ersten Winkelhalbierenden. Dies siehst du hier. Der Funktionsgraph zu $A(x)=x^2$ ist rot und der Graph der Umkehrfunktion (hier: der Wurzelfunktion) ist blau eingezeichnet.

Natürlich kannst du die Umkehrfunktion auch mathematisch herleiten:

$\begin{array}{rclll} y&=&x^2&|&\sqrt{~~~}\\ \sqrt{y}&=&x \end{array}$

Vertausche nun $x$ und $y$. So erhältst du $y=\sqrt x$. Die Umkehrfunktion wird oftmals mit einer $-1$ im Exponenten bezeichnet. Im Zusammenhang ist eindeutig, dass damit die Umkehrfunktion gemeint ist:

$A^{-1}(x)=\sqrt x$

Nun kannst du auch die Seitenlänge des Quadrates mit dem Flächeninhalt $25~\text{cm}^2$ berechnen. Diese beträgt $A^{-1}(25)=\sqrt{25}=5~[\text{cm}]$.

Die Kubikwurzel als Umkehrung einer kubischen Funktion

Das Volumen eines Würfels wird bekanntlich durch die Potenzfunktion $V(x)=x^3$ angegeben.

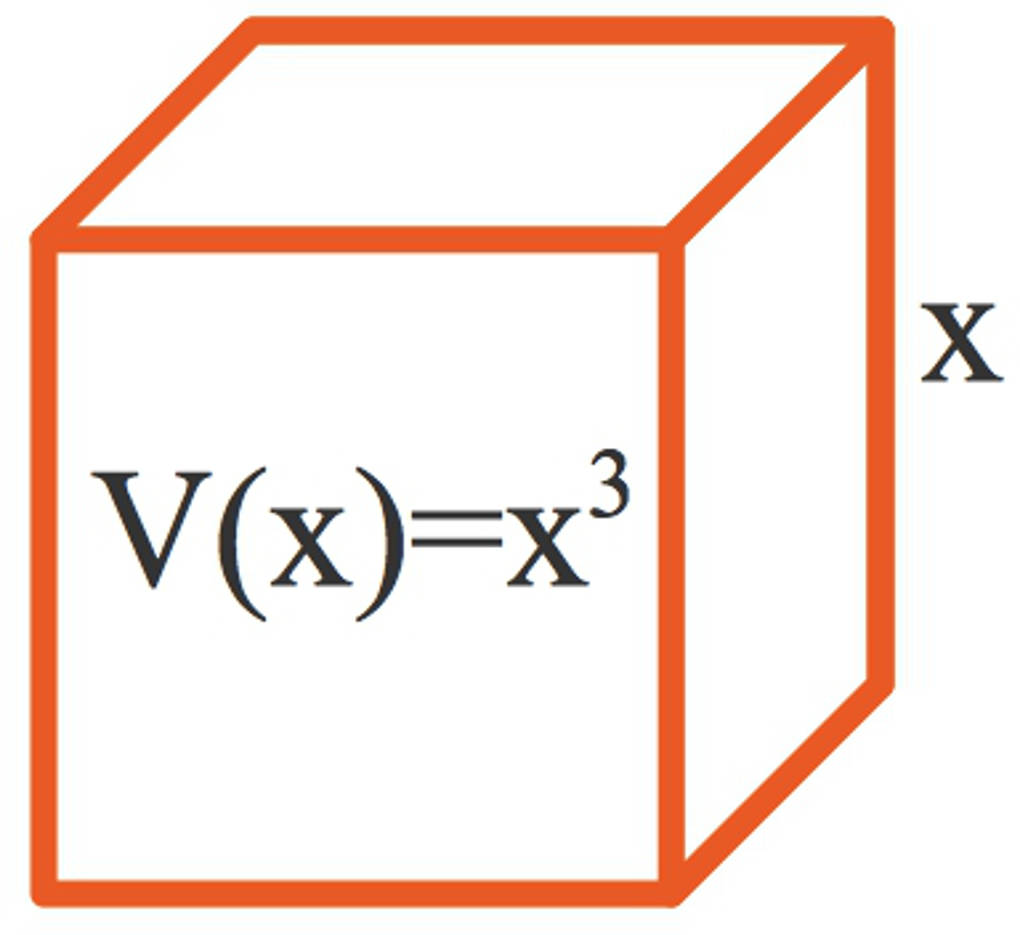
Hier steht $V(x)$ für das Volumen (zum Beispiel in $\text{cm}^3$) und $x$ für die Seitenlänge (in $\text{cm}$). Den zugehörigen Funktionsgraphen kannst du hier in roter Farbe sehen.

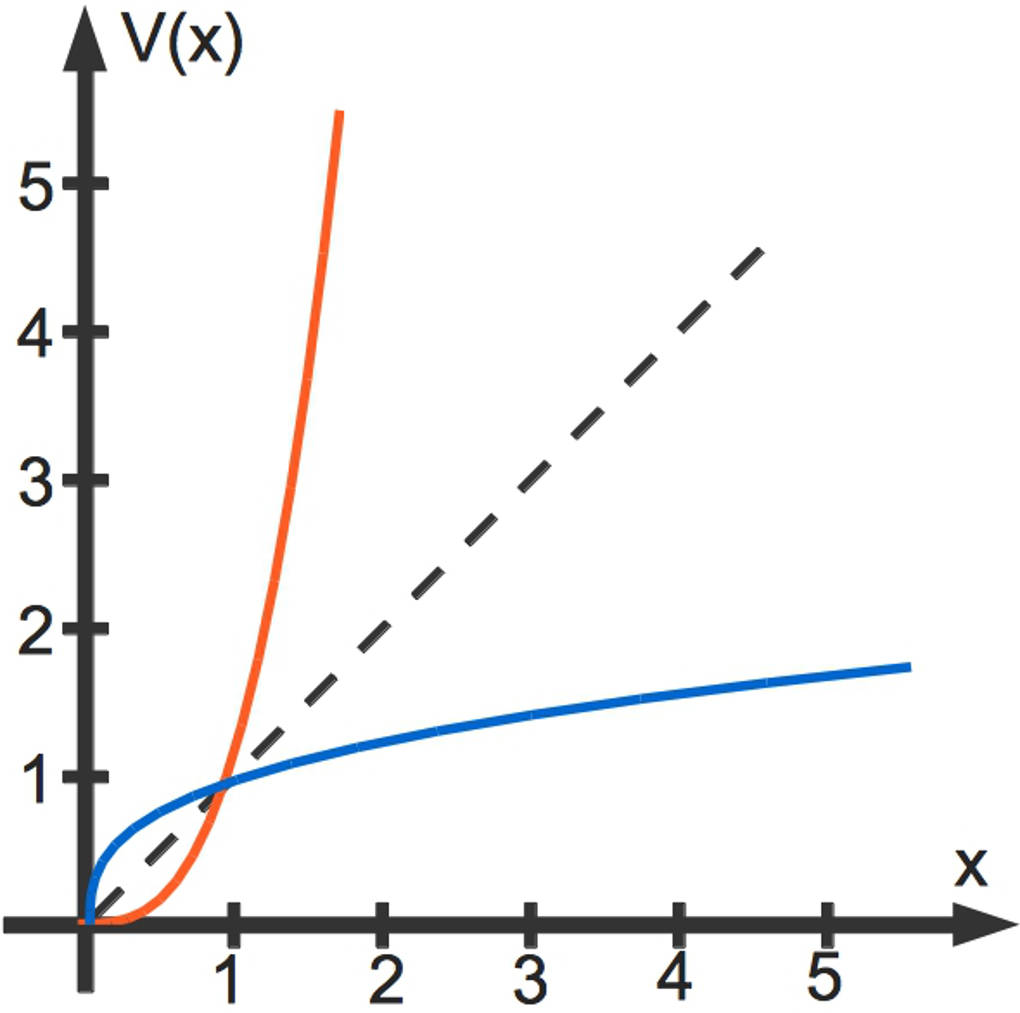
Durch Spiegelung an der ersten Winkelhalbierenden erhältst du den Graphen der Umkehrfunktion, hier in blauer Farbe.

Hier siehst du die mathematische Herleitung:

$\begin{array}{rclll} y&=&x^3&|&\sqrt[3]{~~~}\\ \sqrt[3]{y}&=&x. \end{array}$

Wieder werden $x$ und $y$ vertauscht: $y=\sqrt[3] x$. Die Umkehrfunktion wird so ausgedrückt:

$V^{-1}(x)=\sqrt[3] x$

Wenn du also wissen willst, wie lang die Seite eines Würfels mit dem Volumen $27~\text{}^3$ ist, setzt du $x=27$ in die Umkehrfunktion ein:

$V^{-1}(27)=\sqrt[3]{27}=3$

Die Seitenlänge des Würfels beträgt also $3~\text{cm}$.

Die Umkehrung einer Hyperbelfunktion

Die Umkehrung einer Hyperbelfunktion wird seltener durchgeführt. Es funktioniert aber fast analog. Dies ist einer Hyperbelfunktion der Ordnung $2$:

$f(x)=\frac1{x^2}$

Es muss allerdings $x>0$ sein, da die Division durch $0$ nicht möglich ist. Kehren wir die Funktion um:

$\begin{array}{rclll} y&=&\frac1{x^2}&|&\cdot x^2\\ y\cdot x^2&=&1&|&:y\\ x^2&=&\frac1y&|&\sqrt{~~~}\\ x&=&\frac1{\sqrt y} \end{array}$

Vertauschen von $x$ und $y$ sowie Ersetzen von $y$ durch $f^{-1}$ führt zu der Umkehrfunktion $f^{-1}(x)=\frac1{\sqrt x}$.

Hier siehst du die Funktionsgraphen von $f(x)$ (rot) sowie der zugehörigen Umkehrfunktion $f^{-1}(x)$ (blau).

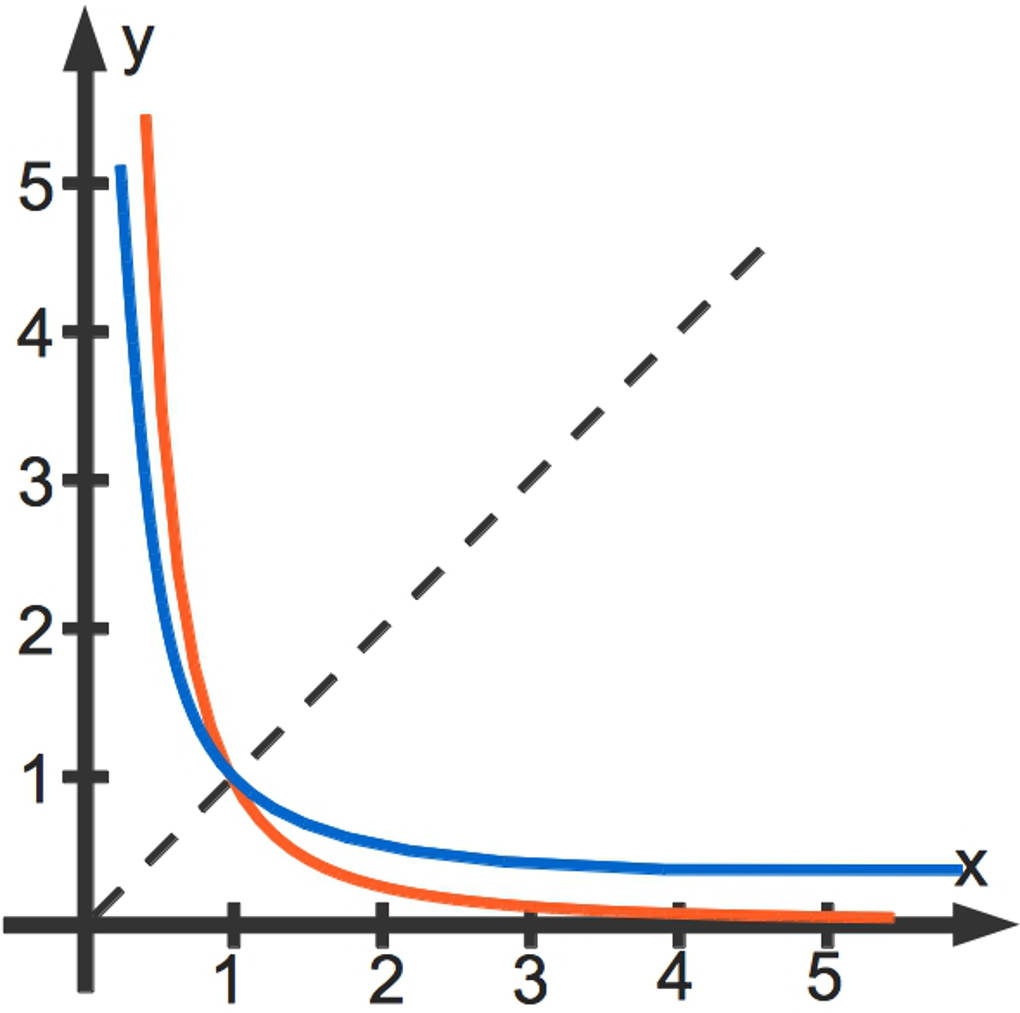
Anwendungsbeispiel

Paul möchte seiner Schwester zum Geburtstag einen Würfel aus festem Pappkarton schenken. Da viele Stifte und auch sonstige Dinge, die seine Schwester für die Schule braucht, in den Karton hineinpassen müssen, soll das Volumen $3375~\text{cm}^3$ betragen.

Der Würfel ist nach oben offen. Paul möchte nun berechnen wie viel $\text{cm}^2$ Pappkarton er für diesen Würfel benötigt. Dabei vernachlässigt er den Verschnitt, also das Papier, was er am Ende wegwirft.

Da der Würfel nach oben offen ist, ist die Gesamtfläche (der Materialbedarf) gegeben durch fünf Quadrate. Jedes dieser Quadrate hat die gleiche Seitenlänge wie der Würfel.

• Paul verwendet die Kubikwurzel zur Berechnung der Seitenlänge: $x=\sqrt[3]{3375~\text{cm}^3}=15~\text{cm}$.
• Nun kann er den Flächeninhaltes eines Quadrates berechnen: $A(15~\text{cm})=(15~\text{cm})^2=225~\text{cm}^2$.
• Zuletzt multipliziert er diese Fläche mit $5$, da er ja fünf solcher Quadrate benötigt: $5\cdot 225~\text{cm}^2=1125~\text{cm}^2$.

Paul kann jetzt in eine Papeterie gehen. Er muss mindestens $1125~\text{cm}^2$ Pappkarton einkaufen.