Winkel
Ein Winkel wird von zwei Strahlen (Halbgeraden) begrenzt, die einen gemeinsamen Ausgangspunkt haben.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Definition des Winkels
- Konstruktion eines Winkels
- Winkelmaß und Winkeleinheiten
- Arten von Winkeln
- Spezielle Winkelpaare
- Steigungswinkel
Definition des Winkels
Ein Winkel wird von zwei Strahlen (Halbgeraden) begrenzt, die einen gemeinsamen Ausgangspunkt haben. Diese Strahlen werden auch Halbgeraden genannt. Der Ausgangspunkt wird als Scheitelpunkt oder Scheitel bezeichnet. Die Strahlen werden auch als Schenkel bezeichnet.
Winkel werden oft mit griechischen Buchstaben wie $\alpha$ (alpha), $\beta$ (beta), $\gamma$ (gamma) oder $\delta$ (delta) bezeichnet.
Konstruktion eines Winkels
Wie messe und zeichne ich Winkel? Winkel können auch mithilfe des Geodreiecks konstruiert werden. Dazu wird die Nullstelle des Geodreiecks auf den Scheitelpunkt des ersten Schenkels gelegt, sodass der Schenkel auf der Hypotenuse liegt. Dann kann anhand der Winkelmarkierungen auf dem Geodreieck ein Punkt eingezeichnet werden, welcher dann mit dem Scheitelpunkt verbunden wird: Es ergibt sich der zweite Schenkel, der den Winkel festlegt. Achte darauf, den Winkel mithilfe der richtigen Winkelmaße abzutragen. Entweder misst du den Winkel
- gegen den Uhrzeigersinn (der 1. Schenkel zeigt nach rechts) oder
- im Uhrzeigersinn ab (der 1. Winkel zeigt nach links).
Genauso lassen sich auch Winkel messen. Ein Schenkel liegt auf der Hypotenuse der Geodreiecks, sodass der Scheitelpunkt des Winkels auf der Nullstelle des Geodreiecks liegt. Dann untersuchst du, welche Stelle der Winkelmarkierungen auf dem Geodreieck der andere Schenkel durchläuft. Hier liest du den zugehörigen Wert ab. Achte auch hier darauf, die richtigen Winkelmaße abzulesen.
Winkelmaß und Winkeleinheiten
Das Winkelmaß dient zur Angabe der Winkelweite. Als Referenz nimmt man den Vollwinkel, der eine Größe von $360^\circ$ hat. Winkel kann man entweder im Grad- oder im Bogenmaß angeben. Dabei entspricht ein Winkel $\alpha$ von $360^\circ$ im Gradmaß einem Winkel $x$ von $2\pi$ im Bogenmaß. Das Bogenmaß gibt die Länge der Kreislinie eines Kreissektors mit Radius $1$ und Winkel $\alpha$ an.
- Allgemein kann man einen Winkel $\alpha$ im Gradmaß durch die Formel $x=\frac{\alpha}{360^\circ}\cdot 2\pi$ ins Bogenmaß $x$ umrechnen. Ein Winkel von $90^\circ$ im Gradmaß entspricht einem Winkel im Bogenmaß von $\frac{90^\circ}{360^\circ}\cdot 2\pi=\frac{\pi}{2}$.
- Wenn du einen Winkel $x$ im Bogenmaß in einen Winkel $\alpha$ ins Gradmaß umwandeln willst, dann kannst du die Formel $\alpha=\frac{x}{2\pi}\cdot 360^\circ$ verwenden. Ein Winkel von $\pi$ im Bogenmaß entspricht einem Winkel von $\frac{\pi}{2\pi}\cdot 360^\circ=180^\circ$ im Gradmaß.
Arten von Winkeln
Winkel werden entsprechend ihrer Größe in unterschiedliche Arten von Winkeln unterteilt:
- Nullwinkel haben eine Größe von $0^\circ$.
- Spitze Winkel sind kleiner als ein Viertel Vollkreis und somit kleiner als $90^\circ$ bzw. $\frac{\pi}{2}$.
- Rechte Winkel haben eine Größe von genau einem Viertel Vollwinkel, was genau $90^\circ$ bzw. $\frac{\pi}{2}$ entspricht.
- Stumpfe Winkel sind größer als ein Viertel Vollwinkel aber kleiner als ein halber Vollwinkel. Die Winkelgröße liegt also zwischen $90^\circ$ und $180^\circ$ bzw. $\frac{\pi}{2}$ und $\pi$.
- Gestreckte Winkel haben eine Größe von genau einem halben Vollwinkel, was genau $180^\circ$ bzw. $\pi$ entspricht.
- Vollwinkel oder volle Winkel haben genau eine Größe von $360^\circ$ bzw. $2\pi$.
Spezielle Winkelpaare
Winkel können in besonderen Beziehungen zueinander stehen. Sie heißen dann Nebenwinkel, Scheitelwinkel, Stufenwinkel oder Wechselwinkel. Schauen wir uns die verschiedenen Winkel einmal anhand der Abbildung genauer an:
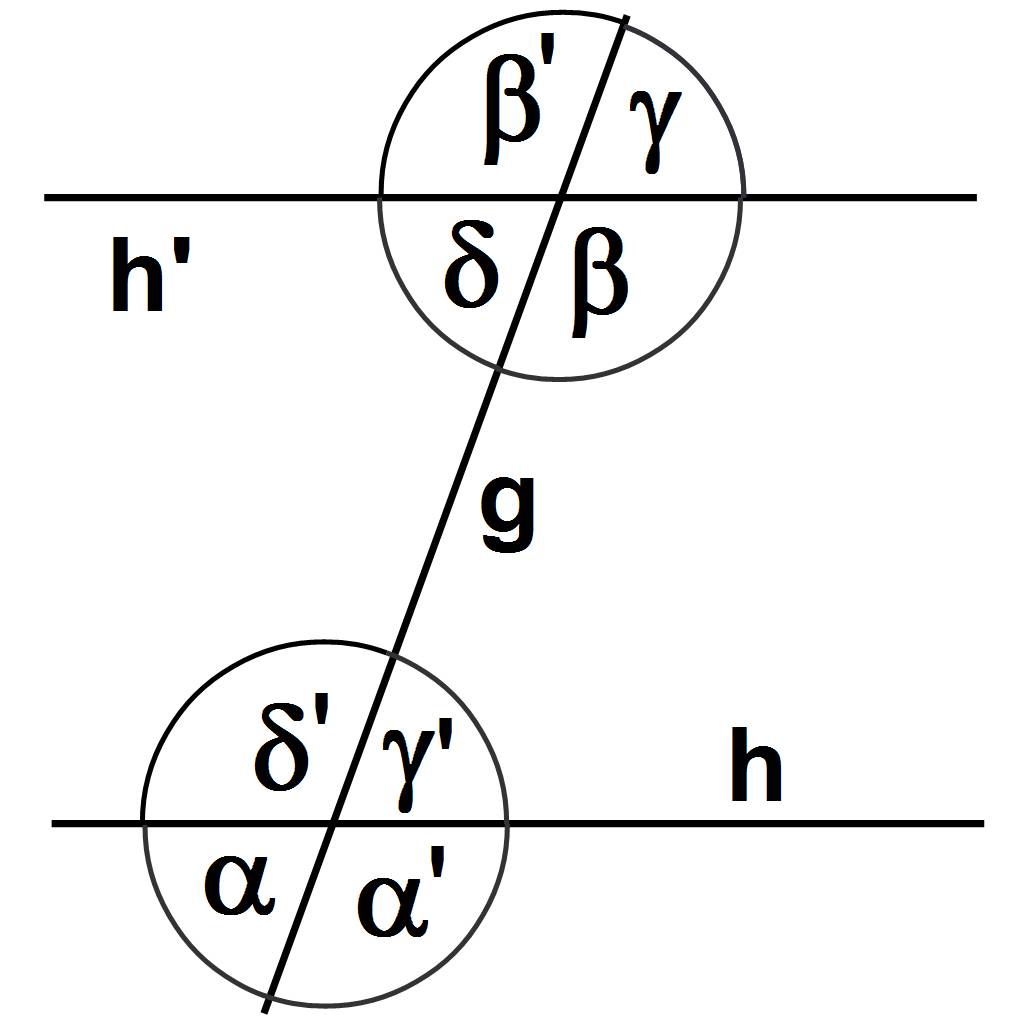
- Nebenwinkel Benachbarte Winkelpaare an sich schneidenden Geraden werden als Nebenwinkel bezeichnet. Sie ergänzen sich zu $180^\circ$. Beispielsweise sind die Winkel $\alpha$ und $\alpha’$ im Bild Nebenwinkel.
- Scheitelwinkel: Wenn sich zwei Geraden schneiden, so werden einander gegenüberliegende Winkelpaare Scheitelwinkel genannt. Sie sind immer gleich groß. Die Winkel $\beta$ und $\beta’$ sind zum Beispiel Scheitelwinkel.
- Stufenwinkel: Wenn eine Gerade $g$ zwei parallele Geraden $h$ und $h’$ schneidet, dann werden Winkel, die auf derselben Seite von $g$ und auf einander entsprechenden Seiten von $h$ bzw. $h’$ liegen, als Stufenwinkel bezeichnet. Sie haben jeweils die gleiche Größe. Beispielsweise sind die Winkel $\gamma$ und $\gamma’$ Stufenwinkel.
- Wechselwinkel: Schneidet eine Gerade $g$ zwei parallele Geraden $h$ und $h’$, dann werden Winkel, die auf unterschiedlichen Seite von $g$ und auf entgegengesetzten Seiten von $h$ bzw. $h’$ liegen, als Stufenwinkel bezeichnet. Sie ergänzen sich zu $180^\circ$. Die Winkel $\alpha$ und $\gamma$ sind zum Beispiel Wechselwinkel.
Steigungswinkel
Die Steigung von Funktionsgraphen kann auch durch den Steigungswinkel angegeben werden. Dafür ist die Tangens- und Arcustangensfunktion sehr wichtig. Wenn für eine Funktion $f(x)$ die Steigung mit $m$ beschrieben wird, dann gilt $m=\tan(\alpha)$. Ebenso wird der Winkel $\alpha$ durch $\tan^{-1}(m) = \alpha$ berechnet. Die meisten Taschenrechner besitzen eine solche Funktion.
Zu beachten ist hier, dass die Steigung $m$ und der Steigungswinkel $\alpha$ nicht proportional zueinander sind. Du kannst also nicht einen Dreisatz verwenden, der Steigung und Steigungswinkel miteinander in Beziehung setzt. Ein Steigungswinkelproblem hast du, wenn du den Steigungswinkel in einem Punkt bestimmen musst.
Alle Videos zum Thema
Videos zum Thema
Winkel (8 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Winkel (8 Arbeitsblätter)
-
 Was ist ein Winkel?
PDF anzeigen
Was ist ein Winkel?
PDF anzeigen -
 Messen und Zeichnen von Winkeln
PDF anzeigen
Messen und Zeichnen von Winkeln
PDF anzeigen -
 Rechter Winkel
PDF anzeigen
Rechter Winkel
PDF anzeigen -
 Arten von Winkeln
PDF anzeigen
Arten von Winkeln
PDF anzeigen -
 Winkel im Kreis
PDF anzeigen
Winkel im Kreis
PDF anzeigen -
 Supplementär- und Komplementärwinkel
PDF anzeigen
Supplementär- und Komplementärwinkel
PDF anzeigen -
 Scheitelwinkel, Nebenwinkel, Stufenwinkel, Wechselwinkel
PDF anzeigen
Scheitelwinkel, Nebenwinkel, Stufenwinkel, Wechselwinkel
PDF anzeigen -
 Winkelpaare an Geradenkreuzungen
PDF anzeigen
Winkelpaare an Geradenkreuzungen
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Quadratische Gleichungen – Übungen
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel















