Polarkoordinaten bei der Kreisbewegung

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
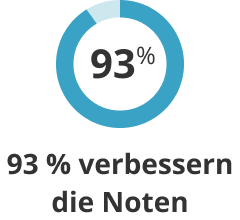
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Polarkoordinaten bei der Kreisbewegung
In diesem Video lernst du die Polarkoordinaten kennen. Polarkoordinaten sind ein „neues“ Koordinatensystem, das einen Punkt in der Zahlenebene nicht wie bisher durch zwei Punkte, sondern durch einen Radius und einen Winkel beschreibt. Es handelt sich also um ein alternatives Koordinatensystem neben dem schon bekannten kartesischen Koordinaten. Wozu man das eigentlich braucht, welche Vorteile die Polarkoordinaten haben und wie man sie wieder in kartesische Koordinaten umrechnet, erfährst du im Video.
Transkript Polarkoordinaten bei der Kreisbewegung
Hallo und herzlich willkommen zum Video über die mathematischen Grundlagen der Kreisbewegung. Unser Thema lautet heute: Polarkoordinaten. Was zum Henker sind Polarkoordinaten? Nehmen wir uns erst mal ein zweidimensionales kartesisches Koordinatensystem mit einer x- und einer y-Achse vor. Ein Punkt in dieser Ebene wird eindeutig durch 2 Zahlen beschrieben, eine für x und eine für y. So funktioniert das bereits bekannte kartesische Koordinatensystem. Das Polarkoordinatensystem funktioniert so: Man kann einen Punkt in dieser Ebene auch durch 2 andere Zahlen beschreiben, und zwar durch eine Länge und einen Winkel. Das sind die Polarkoordinaten. Die Länge nennt man meistens r und den Winkel meistens φ. Die Polarkoordinaten sind sehr, sehr praktisch, wenn wir eine Bewegung auf einer Kreisbahn beschreiben wollen, da sich eine der Koordinaten nicht ändert, nämlich der Radius. Wir brauchen also nur eine Gleichung für den Winkel. Würden wir eine Bewegung auf einer Kreisbahn in kartesischen Koordinaten beschreiben wollen, was natürlich auch geht, bräuchten wir 2 Gleichungen, für x eine und für y eine. Diese sind noch dazu wesentlich komplizierter, weil sie Wurzeln und so etwas enthalten. Aus diesem Grund sind die Polarkoordinaten toll. Sie erleichtern uns das Leben enorm, wenn es um Kreisbewegungen geht, und in der Physik geht es meistens um Kreisbewegungen. Von Planetenbahnen bis zum Atom lässt sich fast alles auf Kreisbewegungen reduzieren, aus diesem Grund unbedingt verinnerlichen. Schauen wir an, wie wir, wenn wir die Polarkoordinaten haben, wieder in unser vertrautes kartesisches Koordinatensystem zurückgelangen. Dazu müssen wir x und y irgendwie durch r und φ ausdrücken. Das ist gar nicht so schwer. Dieser Kreis hier erinnert nämlich sehr an den Kreis, an dem Sinus und Cosinus definiert worden ist. Man kann zum Beispiel hier ein Dreieck zeichnen. Die Hypotenuse ist ja r, der Radius und diese Strecke hier ist der x-Wert. Dann wissen wir: cos(φ)=Ankathete/Hypotenuse=x/r, also ist x=r×cos(φ). Genau das Gleiche können wir auch mit der y-Achse machen: sin(φ)=Gegenkathete/Hypotenuse und die Gegenkathete ist ja y, also, sin(φ)=y/r, also ist y=r×sin(φ). Und damit sind wir schon fertig. Kennen wir also eine Bewegung in Polarkoordinaten, wissen wir jetzt sofort auch die Bewegung in kartesischen Koordinaten. Das war's mit den mathematischen Grundlagen, ich hoffe, dir nützen sie was. Damit bedanke ich mich und bis zum nächsten Mal.
Polarkoordinaten bei der Kreisbewegung Übung
9.244
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.669
Lernvideos
37.113
Übungen
32.360
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt

 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen






