Graphisches Ableiten – Übung (2)

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Graphisches Ableiten – Übung (2)
Willkommen zum zweiten Übungsvideo, in dem ich dir zeigen möchte, wie du eine Winkelfunktion ( auch: trigonmetrischen Funktion ) graphisch ableitest. Dazu wiederholen wir kurz fünf wichtige Regeln zum Ableiten. Anschließend leiten wir die Funktionen sin(x) und cos(x) gemeinsam graphisch ab. Kannst du dich noch daran erinnern, wie die Ableitungen dieser beiden Funktionen aussehen. Oder hattest du das Thema vielleicht noch gar nicht. Dann lernst du ja im Video – ganz nebenbei – noch etwas zu Winkelfunktionen. Viel Spaß dabei!
Transkript Graphisches Ableiten – Übung (2)
Hallo! Heute üben wir gemeinsam, wie du aus dem Graphen einer Winkelfunktion die dazu gehörige Ableitungsfunktion zeichnen kannst.
Regeln beim Ableiten
Beim Ableiten musst du dir allgemein folgendes merken:
- An den Extremstellen der Ursprungsfunktion f(x) ist die Steigung gleich null. Daher hat die Ableitungsfunktion f'(x) hier Nullstellen.
- An den Wendestellen der Ursprungsfunktion f(x) ist die Steigung maximal bzw. minimal. Daher hat die Ableitungsfunktion f'(x) hier Extremstellen.
- Eine positive Steigung an einer Stelle der Ursprungsfunktion führt bei der Ableitungsfunktion zu einem positiven y-Wert an dieser Stelle.
- Eine negative Steigung an einer Stelle der Ursprungsfunktion führt bei der Ableitungsfunktion zu einem negativen y-Wert an dieser Stelle.
- Die Steigung der Ursprungsfunktion an der Stelle x1, ist der Funktionswert der Ableitungsfunktion an dieser Stelle x1.
Ableitung Sinus-Funktion
Als Beispiel schauen wir uns einmal den Graphen der Sinus-Funktion an. Diese Funktion ist, wie du sicherlich weißt, periodisch, mit einer Periodenlänge von 2 Pi. Da die Sinus-Funktion an den Stellen minus Pi halbe, bei Pi Halbe und bei 1,5 Pi Extremstellen hat, besitzt die zugehörige Ableitungsfunktion an diesen Stellen ihre Nullstellen.
Die Wendestellen des Graphen der Sinusfunktion sind minus Pi, 0, plus pi und 2 pi. Dort sind dann bei der zugehörigen Ableitungsfunktion die Extremstellen.
Nun musst du nur noch die Steigungen der Ursprungsfunktion f(x) = sin(x) anschauen. Ist die Steigung positiv, dann verläuft der Graph der Ableitungsfunktion oberhalb der x-Achse. Ist die Steigung negativ, dann verläuft der Graph der Ableitungsfunktion unterhalb der x-Achse.
Es entsteht nun folgender Graph. Schau ihn dir genau an. Fällt dir vielleicht etwas auf? Es ist der Graph der Kosinus-Funktion.
Es gilt also: Die Ableitungsfunktion der Sinus-Funktion ist die Kosinus-Funktion. Oder anders ausgedrückt: f(x) = sin(x) ist f'(x) = cos(x).
Ableitung Kosinus-Funktion
Dann wollen wir mal schauen, ob die Kosinus-Funktion genauso einfach differenziert werden kann. Dies machen wir aber nun etwas schneller. Schau dir erst noch einmal den Graphen der Kosinus-Funktion an.
Bei minus Pi, bei 0, plus pi und bei 2 pi sind hier die Extremstellen, also hat die Ableitungsfunktion dort die Nullstellen.
Die Wendestellen der Kosinus-Funktion befinden sich bei minus Pi halbe, bei Pi Halbe und bei 1,5 Pi, dort hat unsere Ableitungsfunktion die Extremstellen.
Nun musst du nur noch die Steigungen der Ursprungsfunktion f(x) = cos(x) anschauen. Ist die Steigung positiv, dann verläuft der Graph der Ableitungsfunktion oberhalb der x-Achse. Ist die Steigung negativ, dann verläuft der Graph der Ableitungsfunktion unterhalb der x-Achse.
Schauen wir uns unsere Ableitungsfunktion zur Kosinus-Funktion an, so kann man folgendes erkennen: Es handelt sich um eine Sinus-Funktion die an der x-Achse gespiegelt wurde. Somit gilt: Die Ableitung der Funktion f(x) = cos(x) ist f'(x) = -sin(x).
Zusammenfassung
So, das war es mal wieder für heute. Wir haben gelernt, dass man auch Winkelfunktion graphisch ableiten kann. Dabei gilt die Merkregel in Kurzform: sin'(x) = cos(x) und cos'(x) = -sin(x)
Ich wünsche dir noch einen schönen Tag! Wir sehen uns bestimmt bald wieder!
Graphisches Ableiten – Übung (2) Übung
-
Bestimme den Ableitungsgraphen der Sinusfunktion.
-
Benenne markante Punkte des Ableitungsgraphen.
-
Entscheide, bei welchem Graphen es sich um den der Ableitungsfunktion handelt.
-
Zeige markante Punkte des Ableitungsgraphen.
-
Gib wichtige Regeln zum graphischen Ableiten wieder.
-
Prüfe die Aussagen über den Graphen der zweiten Ableitung.
9.311
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.718
Lernvideos
37.183
Übungen
32.414
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Quadratische Gleichungen – Übungen
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel

 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen



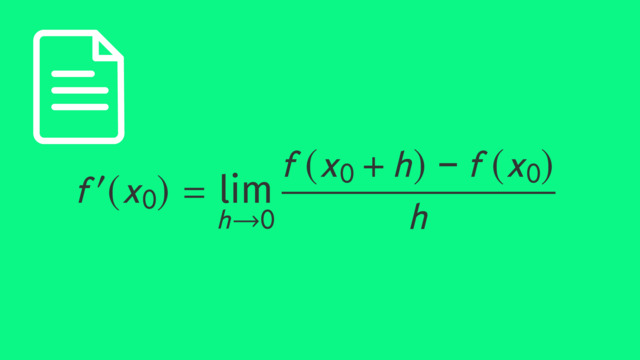




Hallo Hangu,
du hast damit vollkommen recht. f''''(x) ist dann wieder sin(x).
Viele Grüße aus der Redaktion